This page was last modified 2007-02-15 09:41:59 by Puchu.Net user Choco. (Show history)

Homogeneous notation is used during transformations of both vectors and points. In homogeneous coordinates a point or a vector is expressed as .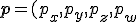

Contents 1 Points and Vectors 2 Homogeneous Form 3 Homogenization 4 References

Points and Vectors

Points have component 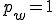and vectors have .

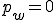Homogeneous Form

Normal rotation, scaling and shear transformation matrices are 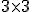, these matrices are augmented into the homogeneous form, a 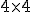matrix that encapsulates all possible transforms we can perform:

A translation matrix that translates a point by a vector 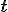is:

Matrix-matrix multiplications and matrix-vector multiplications are done following normal rules of matrix operations. By using homogeneous forms when doing calculations, a vector 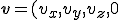is not translated because the last column is zero. This is what we want, because a vector points in a direction and therefore translation has no meaning. However, if last column is one, then it is a point affected by the homogeneous transform. Using homogeneous coordinates to represent both points and vectors, and always using transformation matrices in homogeneous forms allow us to work with points and vectors in the same manner.

Homogenization

In projections, 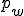has values other than 0 or 1, and the actual coordinate of the point is done through homogenization, or dividing all components by 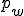. In other words, once we calculate 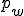, the projected point is then .

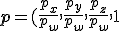References

1. Akenine-Moller, Tomas and Eric Haines, Real-Time Rendering 2nd Edition, A K Peters: 731-732.
2. Wikipedia contributors. Homogeneous coordinates. Feb. 15, 2007 <http://en.wikipedia.org/wiki/Homogeneous_coordinates>.